Paradoxical Thinking

Since high school, I've had an obsession with contradictions and paradoxes. If I had to pinpoint any one thing to think about for the rest of time, it'd be intersections of contradictions.

From a purely logical standpoint, contradictions shouldn't exist. Yet we hear them all the time, summarized in captivating symbols or short aphorisms: "empty space is what makes a bowl useful", "be strong yet weak", etc.

Why are they so ubiquitous, in spite of their impossibility? Being a math person, this question plagued me, until I figured out how to reconcile some types of contradictions. What I show below is more a useful analytical framework for understanding contradictory phenomena than a concrete analysis of complexity or contradictions.

Frames of reference

Many types of contradictions can be resolved by looking at different frames of reference (FOR). There may be other types of contradictions that don't buckle under the "FOR attack" but I've found this idea to be helpful for pinpointing what causes contradictory behavior.

An object can simultaneously exhibit one property at one FOR but the opposite property at another FOR. The key insight is that descriptions apply only for specific FORs.

I can call Chicago and New York "close" when looking at a map, but when I ditch the map and go walking from Chicago to New York, Chicago and New York are "far apart". This means that when describing something, we need to ensure that we include which FOR we are in.

Size variation

My favorite method of changing FORs is altering the size of the frame window a.k.a. size variation. This is an obvious method - of course things look different when you look at them closely vs. at a distance!

Although deceivingly simple and almost stupid, this idea isn't completely useless. For example, a circle is circular when viewed through a large frame window, but the circle "straightens out" into a line at a sufficiently small frame window. In this way, a circle is "both" linear and circular.

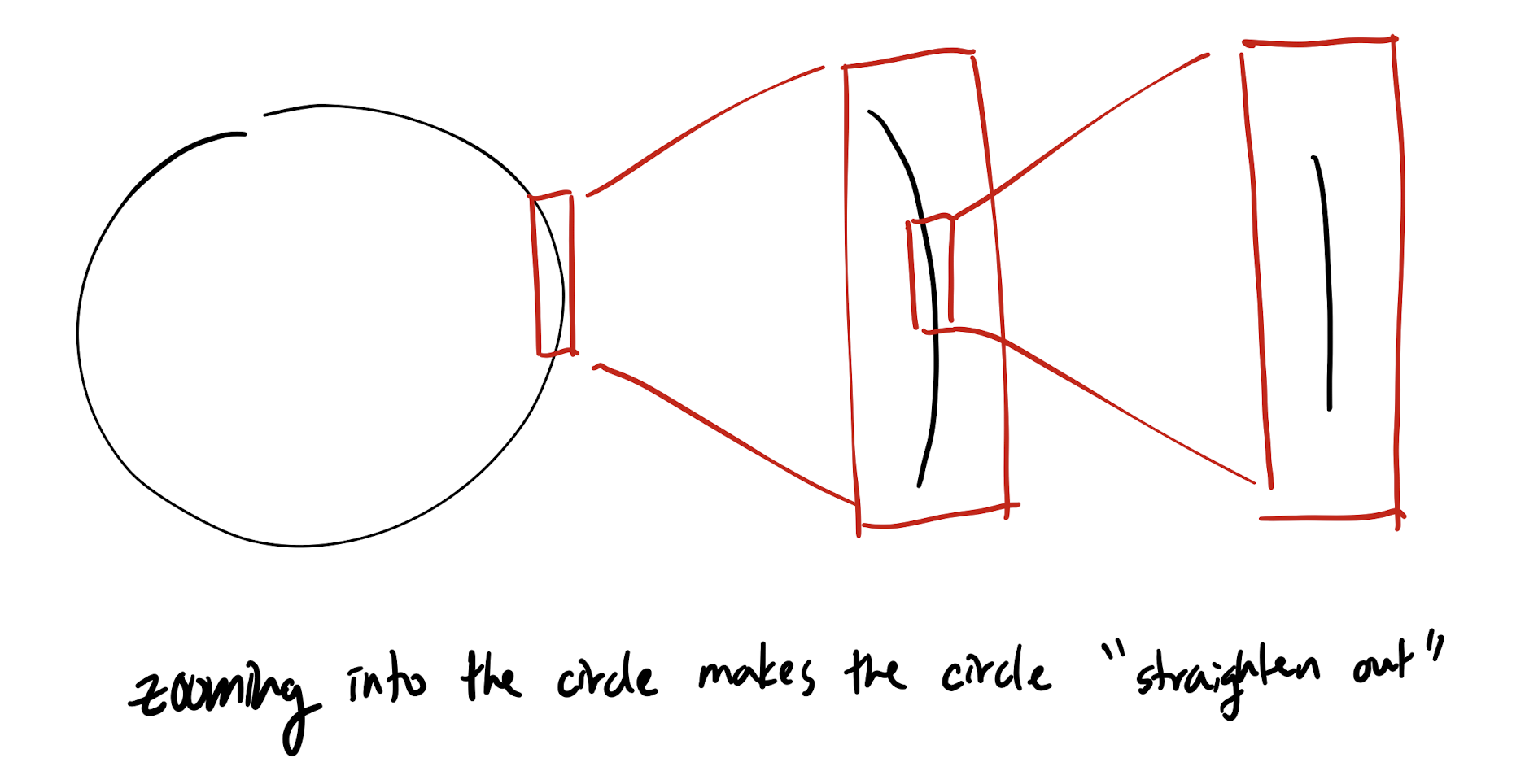
In fact, a curved object exhibiting both circular and linear properties by way of varying FOR size is the inspiration for using derivatives to approximate differentiable curves. Generally, linearity lends itself to easier computation, so having a linear approximation for a complex, bendy curve can be incredibly useful (given a reasonable error margin, of course).

Positive-negative variation

Another useful variation is the positive-negative variation.

The name of this variation derives from the artistic notion of positive and negative space. The positive space of the Mona Lisa consists of the Mona Lisa herself, while the negative space is the faded trees and hills in the background.

To apply positive-negative variation, break an object or concept down into its consituent parts. As an example, consider societies. The constituent parts (i.e. individuals) of a society come together and form relationships in order to form the whole. The "positive space" of the society then consists of its individuals, while the "negative space" consists of the relationships between them.

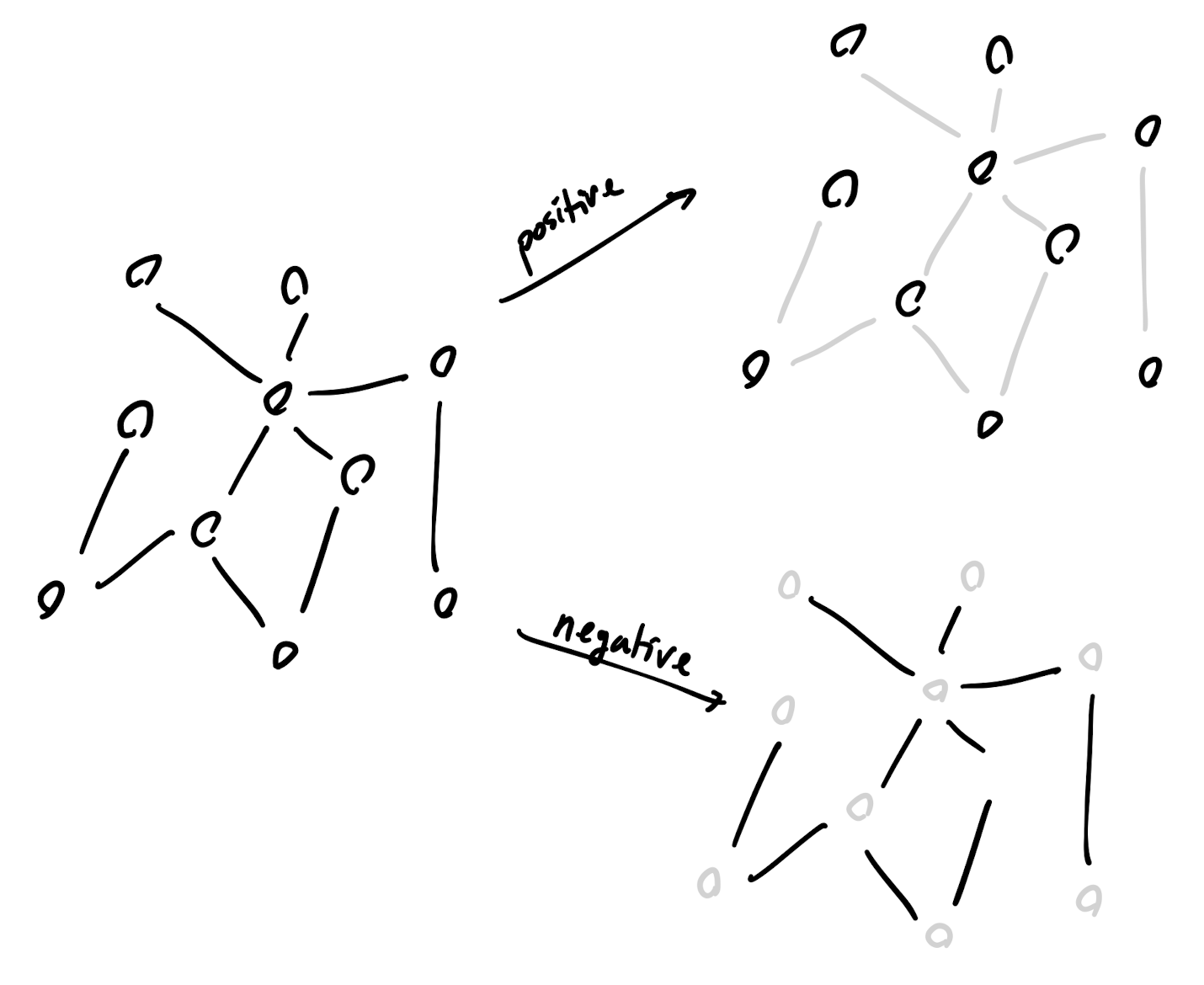
Positive-negative variation is easily visualized by taking any network and breaking it down into its nodes and edges. The positive space is just the nodes without the edges, and likewise the negative space is the edges without the nodes.From a positive FOR, the properties of the nodes become visible. The negative FOR reveals how nodes behave when they clash with other nodes.

Relative-absolute variation

You can put different variations together to get new flavors. The relative-absolute variation is one such variation - it is the combination of size and positive-negative variation in that it is positive-negative variation viewed on a micro-scale. It addresses the question "How does the essence of an object affect the nature of its existence, and vice versa?".

The insight for relative-absolute variation is that, except for things that live in complete isolation, most objects or concepts have a relative and an absolute definition. The former defines by way of relationships to other things, whereas the latter defines the thing in its own terms.

A relative definition is dependent on other things, while an absolute definition is independent and can stand on its own. For example, the relative definitions of me would be "first son of - and -, brother of -, etc.", while my absolute definition would be "homo sapien".

Notice that the absolute definitions automatically imply any relative definitions, if and when the absolute definitions exist. Wouldn't it be nice if we had absolute definitions for every object and concept, then? Sadly, absolute definitions are hard to find in non-abstract worlds, so relative definitions are usually all we can work with.

Caveat: cross-contaminated FORs

Sometimes, descriptions carry over into other FORs. The tricky bit with relative-absolute variation is that the absolute definition implies the relative defintions.

Example

Sequences are a perfect demonstration of the relative-absolute variation at work.

Assume that a generic metric space \( (E, \rho) \).

\(\text{Definition: }\) A sequence \( \{a_n\} \) converges to \(a \in E \) if for all \( \epsilon > 0 \), there exists \( N \) such that if \( n \geq N \), then \( \rho(a_n, a) < \epsilon \).

\(\text{Definition: }\) A sequence \( \{a_n\} \) is a Cauchy sequence if for all \(\epsilon > 0\), there exists \(N\) such that if \(m, n \geq N\), then \( \rho(a_m, a_n) < \epsilon \).

Notice that a Cauchy sequence gives a relative definition: the convergent-esque behavior of a sequence is determined by the distances between the elements past a certain threshold. On the other hand, the definition of convergence is absolute.

In all cases, convergence implies Cauchy-ness. The converse is not always true, however. This isn't intuitive, as you'd expect elements that get closer and closer to each other to converge to something. Finding a condition for which Cauchy-ness implies convergence is then a non-trivial task.

Luckily, we know what that condition is. The spaces where the converse holds are called complete metric spaces. In complete metric spaces, Cauchy sequences and convergent sequences are equivalent; the relative definition equals the absolute definition.

This is highly unusual. It's very rare for relative and absolute definitions to match up. Things like complete metric spaces don't pop up often in the natural/social world, so I haven't found a social analogue for complete metric spaces yet.